第5回『建物にはたらく力と固有周期』では、地震のときに建物にはたらく力と建物の固有周期の関係について説明しました。今回は、その理由についてもう少し詳しく説明したいと思います。
建物の揺れと「共振」の関係
皆さんも「共振」という言葉は聞かれたことがあると思います(波動の世界、特に音の世界では共鳴ともいいます)。これは、二つの音叉の片方をたたくと、もう一方も振動を始めるという現象です。
それと同じような現象が、地震による建物の振動にも大きく関わってきます。それが、第5回で説明した、同じ波でも建物の固有周期によりはたらく力に差ができる原因です。
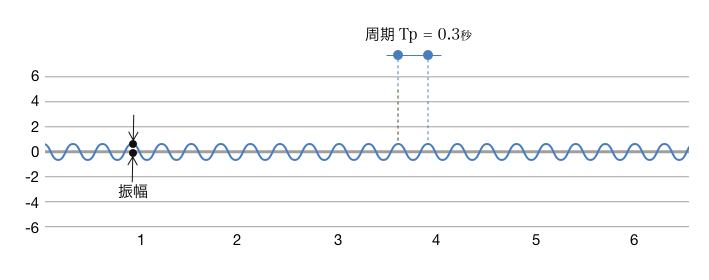
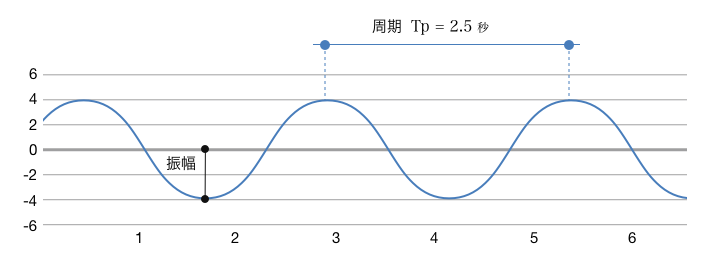
図6-1は、正弦波(sine波)と呼ばれる波を示しています。この波は波の中でも最も単純なもので、図にあるように「振幅」と「周期」が決まれば形が決まります。

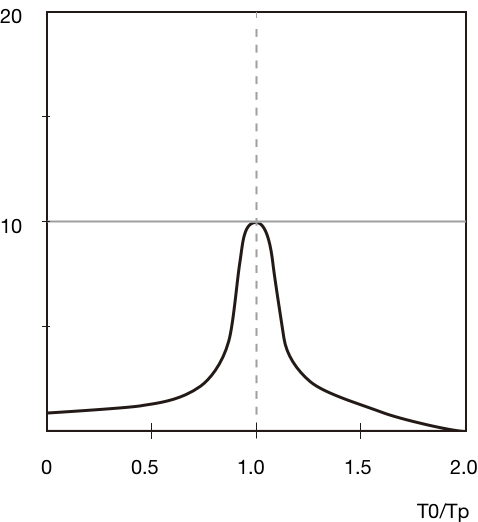
このような波を地震の加速度波形だと考えて、第5回で説明した1質点の建物モデルに作用させて計算したものが図6-2に示したもので、「共振曲線」と呼ばれます(「伝達関数」と呼ばれることもあります)。
横軸は建物の固有周期T0と正弦波の周期Tpの比であり、T0/Tp=1.0が、それが一致した場合、即ち共振を示しています。縦軸は図6-1の振幅が何倍になるかを示す数値です。
図6-2では、建物の減衰が5%のときの値で共振を起こした場合、10倍の振幅になります(「減衰」とは、以前少し説明しましたが、建物が持っている揺れにくさを表す指標で、減衰が0のときは縦軸の倍率は無限大になります)。逆にT0/Tpの値が0.5や1.5になると、ほとんど加速度の増幅は起こりません。
実際の地震に当てはめるには
ただし、自然界にはこのような単純な波は存在しません。第4回『建物にはたらく地震力』でEl Centro 波を紹介しましたが、この波形は時間的に有限ですし、振幅も周期も一定ではありません。したがって、図6-2のようなものを求めることはできません。
そこで考えられたのが、上記の地震波のような不規則な波を、正弦波のような単純な波の足し算に分解する方法(フーリエ変換)です。
この方法を適用すると、図6-3のようなものが得られます。これを「フーリエスペクトル」といいます。横軸は正弦波の周期と考えてください。縦軸はその周期を持つ正弦波の振幅にその地震の継続時間の1/2をかけた数値で、「フーリエ振幅」といいます。
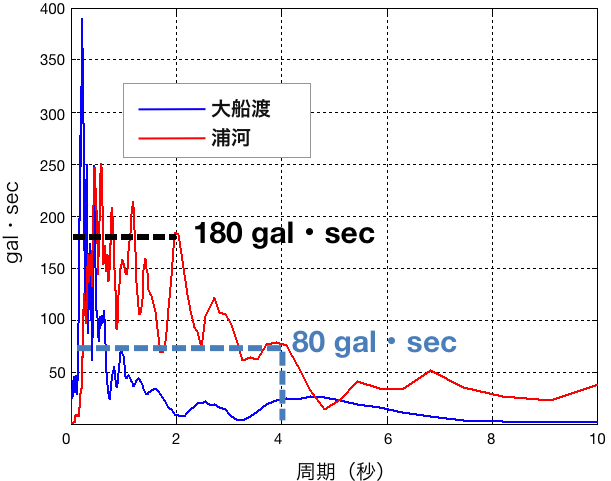
出典:気象庁ホームページ ※一部加工
図6-3の浦河の波では、周期2秒の正弦波に対応する値は180gal・secくらいです。同様に、周期4秒では80gal・secとなります。地震の継続時間はその地震ごとに決まるので、このように、地震波の中にどのような周期の正弦波が多く含まれるか(振幅が大きいか)を調べることができます。
たとえば、図6-2を適用して、固有周期2秒の建物に図6-3の浦河の地震動がはたらくと、建物の固有周期と正弦波の周期が一致する2秒の正弦波は10倍に増幅され、建物には10×180gal・sec÷(地震継続時間/2)の加速度がはたらくことが予想できます。なお、図6-2から、1秒の正弦波や3秒の正弦波はほとんど増幅されないことになります。
長周期地震動とは
最近よく言われる「長周期地震動」というのは、2~2.5秒以上の周期でこのフーリエスペクトルの振幅が大きくなる傾向を持つ地震動波形で、超高層ビルの固有周期が2秒以上となることを考え合わせると、共振を起こす可能性が高くなります。
言い換えるならば、建物は地震動波形の中から、自分と共振しやすい正弦波を選んで揺れる傾向があることになります。したがって、いくら大きな地震でも、その地震動の中に含まれる建物の固有周期と近い正弦波の振幅が小さければ、あまり揺れないということになります。