「固有周期」という言葉をご存じですか?
地震が起きたときに建物がどのような揺れ方をするか、つまり、建物にどの程度の力(地震力)がはたらくかは、地震の揺れの大きさだけでなく、建物によっても大きく変わります。
建物が建っている場所の地面の揺れが同じでも、建物によって揺れ方が異なるのです。
そのことは、地震の被害を受けた町の映像などでお気づきになっているかと思います。隣り合って建っている建物でも、被害の程度は大きく異なるということがありますね。
それでは、どのような建物に、より強い力がはたらくのでしょうか。その決め手になるのが、建物の「固有周期」です。
固有周期とは?
「固有周期」とは、建物が一方に揺れて反対側に戻ってくるまでの時間のことです。
建物を振り子にたとえて考えてみると、わかりやすいかもしれません。
振り子を揺らすと、片側に揺れ、戻ってきます。そのときの、行って戻ってくるまでの時間が固有周期です。
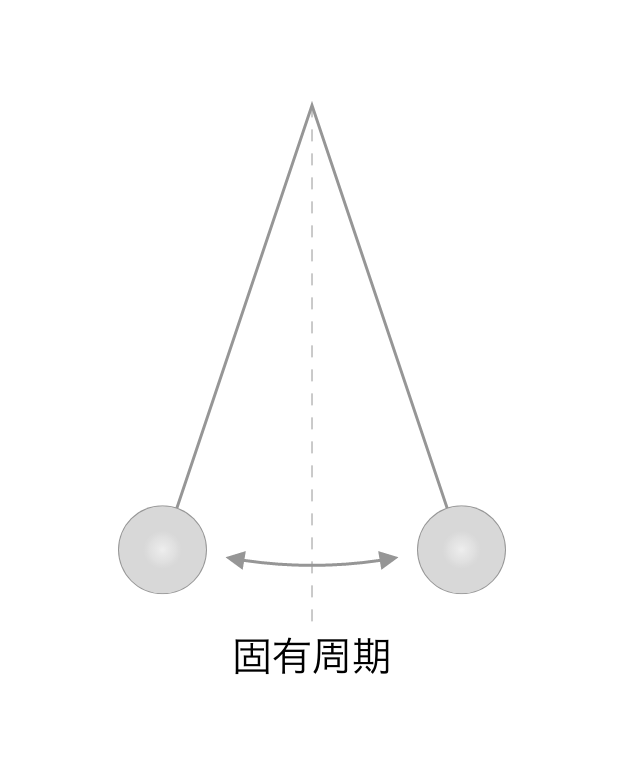
固有周期が長いほど、ゆっくり揺れる
この固有周期が長いほど建物にはたらく力は小さくなり、ゆっくり揺れます。
反対に、固有周期が短いほど建物にはたらく力は大きくなり、小刻みに揺れます。
それでは、固有周期はどのような条件で決まるのでしょうか?
それは、建物の質量・剛性(変形のしやすさ)です。
建物の固有周期
図5-1のように建物をモデル化すると、建物の固有周期は下式で表されます。
\[T = 2\pi\sqrt{m/k}\]\(T\):固有周期 \(m\):質量 \(k\):剛性

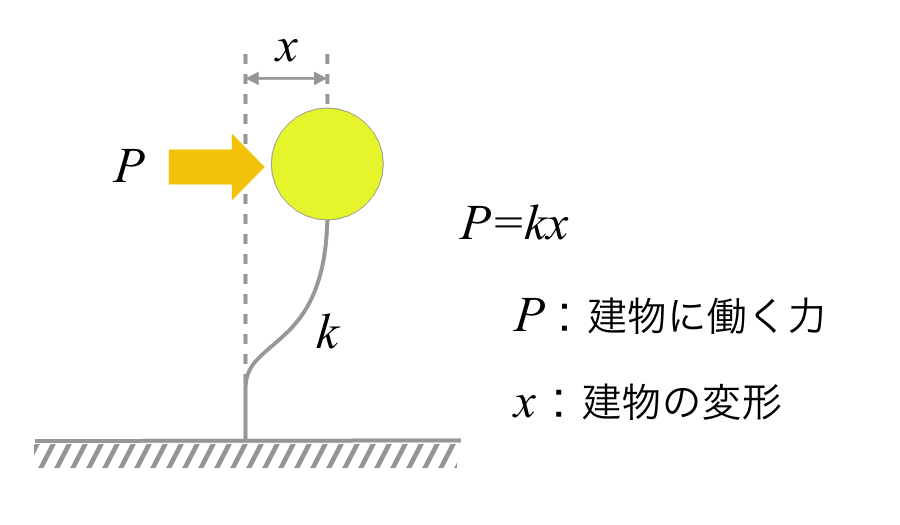
この式から、建物の質量(重量)が大きくなると固有周期は長くなり、剛性が大きくなると固有周期は短くなりことがわかります。ここでいう「剛性」とは、建物の変形のしやすさで図5-2のようにあらわされます。
つまり、「剛性が高い」というのは建物が変形しにくいこと、「剛性が低い」というのは建物が変形しやすいことです。
ただし、図5-1・図5-2は建物を一つの質量を持つ点(質点といいます)に置き換えています。
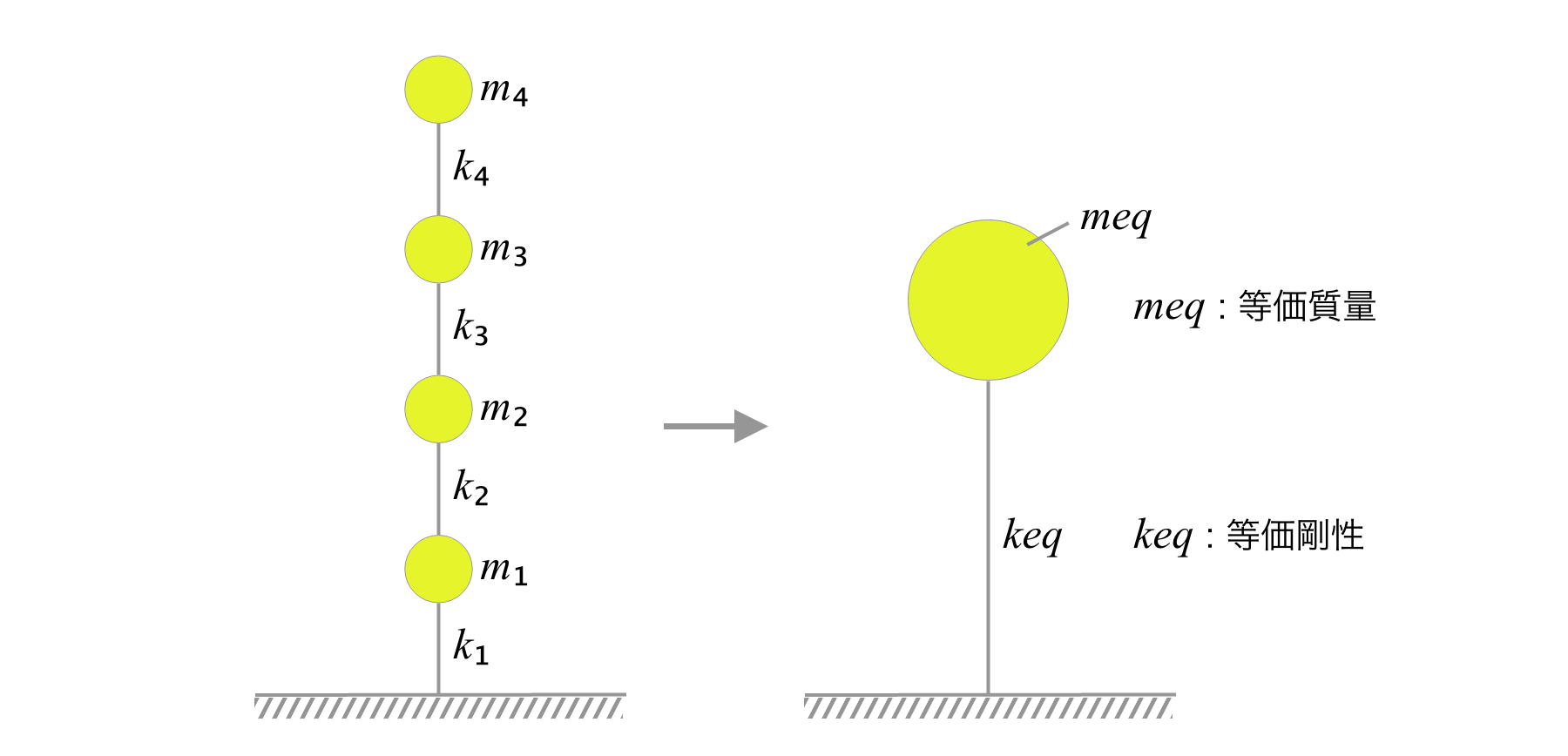
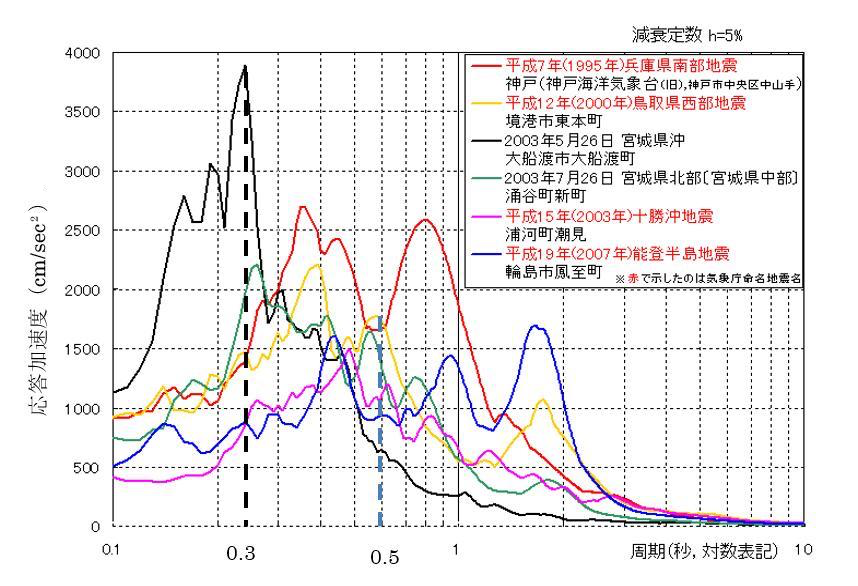
1階建ての建物であればこのモデルによく対応しますが、事務所ビルのように何層にもなる場合、その質点は各階に分散して置いた方がうまく建物を表現できます(図5-3)。
このような何層にもなる建物でも等価な1質点のモデルに置き換え、固有周期を計算することが可能です。その方法はここでは説明しませんが、先ほど述べた質量が大きいほど固有周期が長くなり、剛性が大きくなるほど固有周期が短くなるという性質は変わりません。
なお、図の5-3のように何層にもなる建物の固有周期の計算には、時間と手間がかかります。そのため建築基準法では比較的多く建てられる日本の一般的建築物を対象に建物の高さと関連付けた簡略式が示されています。